In microbiome study, differential abundance analysis (DAA) is an active area of research. Over 12 years ago, the term “differential abundance” was coined as a direct analogy to differential expression from RNA-seq and has been adopted to use in microbiome literature (McMurdie and Holmes 2014; White et al. 2009; Paulson et al. 2013). The main goal of DAA is to identify features (i.e., OTUs, ASVs, taxa, species, etc.) that are differentially abundant across sample groups (i.e., features present in different abundances across sample groups).
Microbiome data are sparse and have many zeros; to appropriately identify features, the models that are used to analyze microbiome data should have the capability to address the issues of overdispersion, zero inflation, and sparsity. To address the overdispersion and zero inflation while identifying the microbial taxa that are associated with covariates, several specifically designed statistical models for microbiome data have been proposed. In this chapter, we first introduce the zero-inflated Gaussian (ZIG) and zero-inflated log-normal (ZILN) mixture models (Sect. 12.1). Then we illustrate the ZILN via the metagenomeSeq package (Sect. 12.2). Sections 12.3 and 12.4 introduce and illustrate some additional statistical tests and some useful functions in metagenomeSeq, respectively. Next, we provide some remarks on CSS, ZIG, and ZILN in Sect. 12.5. Finally, we complete this chapter with a brief summary in Sect. 12.6.
12.1 Zero-Inflated Gaussian (ZIG) and Zero-Inflated Log-Normal (ZILN) Mixture Models
Both ZIG mixture and ZILN models are implemented in the metagenomeSeq package (Paulson 2020) via the functions fitZig() and fitFeatureModel(), respectively. The function fitZig() relies heavily on the limma package (Smyth 2005). The ZIG mixture was proposed first in 2013 (Paulson et al. 2013), which estimates the probability whether a zero for a particular feature in a sample is a technical zero or not. The fitFeatureModel() was later reparametrized to fit a zero-inflated model for each specific OTU separately. Currently the ZILN model along with the fitFeatureModel() is recommended (Paulson 2020).
The proposal of ZIG mixture model was motivated by the observation that the depth of coverage in a sample is directly related to how many features are detected in a sample. It was shown that there exist a relationship between depth of coverage and OTU identification ubiquitous in marker-gene survey datasets. Thus, ZIG mixture model was proposed to use a probability mass to accommodate the excess zero counts (both sampling zeros and structural zeros) and a Gaussian distribution to model the mean group abundance (the nonzero observed counts) for each taxonomic feature to explicitly account for biases in DAA resulting from under-sampling of the microbial community.
The model directly estimates the probability that an observed zero is generated from the detection distribution owing to under-sampling (sampling zeros) or due to absence of the taxonomic feature in the microbial community (structural zeros), i.e., from the count distribution. An expectation-maximization algorithm is used to estimate the expected value of latent component indicators based on sample sequencing depth of coverage.
The model is implemented via the metagenomeSeq package, mainly by implementing two methods: the cumulative sum scaling (CSS) normalization and zero-inflated Gaussian (ZIG) distribution mixture model.
The ZIG mixture model was designed to use the CSS normalization technique to correct the bias in the assessment of differential abundance (DA) introduced by total sum (TSS) normalization.
12.1.1 Total Sum Scaling (TSS)
In RNA-seq and microbiome literature, TSS (Paulson et al. 2013; Chen et al. 2018) and proportion (McMurdie and Holmes 2014; Weiss et al. 2017) are referred as the same method. TSS uses the total read counts for each sample as the size factors to estimate the library size or scale the matrix counts. TSS normalizes count data by dividing taxon or OTU read counts by the total number of reads in each sample to convert the counts to proportion.
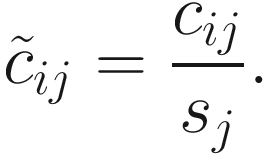
- 1.
TSS is not robust to outliers (Chen et al. 2018), is inefficient to address heteroscedasticity, is unable to address overdispersion, and results in a high rate of false positives in tests for species. This systematic bias increases the type I error rate even after correcting for multiple testing (McMurdie and Holmes 2014).
- 2.
TSS lies on the constant-sum constraint; hence it cannot remove compositionality; instead it is prone to create compositional effects, making nondifferential taxa or OTUs appear to be differential (Chen et al. 2018; Mandal et al. 2015; Tsilimigras and Fodor 2016; Morton et al. 2017).
- 3.
TSS has a poor performance in terms of both FDR control and statistical power at the same false-positive rate, compared to other scaling or size factor-based methods such as GMPR and RLE because of strong compositional effects (Chen et al. 2018).
- 4.
Actually, like to rarefying, TSS or proportion is built on the assumption that the individual gene or taxon count in each sample was randomly sampled from the reads in multiple samples. Thus, counts can be divided by total library size to convert to proportion, and gene expression analysis or taxon abundance analysis can be fitted via a Poisson distribution. Because in both RNA-seq data and 16S rRNA-seq data, the assumption cannot meet, the sample proportion approach is inappropriate for detection of differentially abundant species (McMurdie and Holmes 2014) and should not be used for most statistical analyses (Weiss et al. 2017).
12.1.2 Cumulative Sum Scaling (CSS)
CSS normalization (Paulson et al. 2013) is a normalization method specifically designed for microbiome data. CSS aims to correct the bias in the assessment of differential abundance introduced by total sum normalization. CSS method is to divide raw counts into the cumulative sum of counts, up to a percentile determined using a data-driven approach in order to capture the relatively invariant count distribution for a dataset. In other words, the choices of percentiles are driven by empirical rather than theoretical considerations.
Let 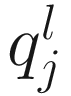 denote the lth quantile of sample j (i.e., in sample j there are l taxonomic features with counts smaller than
denote the lth quantile of sample j (i.e., in sample j there are l taxonomic features with counts smaller than 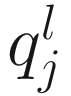 ). For l = ⌊.95 m⌋,
). For l = ⌊.95 m⌋, 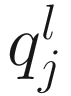 corresponds to the 95th percentile of the count distribution for sample j. Also denote
corresponds to the 95th percentile of the count distribution for sample j. Also denote 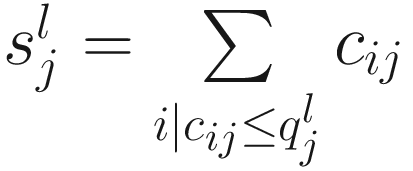 as the sum of counts for sample j up to the lth quantile. Using this notation, the total sum
as the sum of counts for sample j up to the lth quantile. Using this notation, the total sum 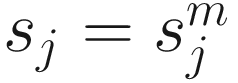 , CSS normalization method chooses a value l ≤ m as a normalization scaling factor for each sample to produce normalized counts
, CSS normalization method chooses a value l ≤ m as a normalization scaling factor for each sample to produce normalized counts  , where N is an appropriately chosen normalization constant.
, where N is an appropriately chosen normalization constant.
In practice, the same constant N (the median is recommended using as scaling factor 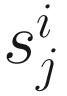 across samples) is used to scale all samples so that normalized counts have interpretable units. Actually, CSS defines the sample-specific count distributions l ≤ m as reference distribution (samples) and interprets counts for other samples as relative to the reference.
across samples) is used to scale all samples so that normalized counts have interpretable units. Actually, CSS defines the sample-specific count distributions l ≤ m as reference distribution (samples) and interprets counts for other samples as relative to the reference.
CSS requires to set the threshold as at least the 50th percentile. Then CSS calculate the normalization factors for samples as the sum over the taxa or OTUs counts up to the threshold. In such way, CSS method optimizes the threshold from the data to minimize the influence of variable high-abundant taxa or OTUs. For example, to mitigate the influence of larger count values in the same matrix column, CSS only scales the portion of each sample’s count distribution that is relatively invariant across samples. CSS normalization can be implemented using metagenomeSeq package. By default, 50th percentile is set as the threshold.
12.1.3 ZIG and ZILN Models
ZIG mixture model assumes that CSS-normalized sample abundance measurements are approximately log-normally distributed given large numbers of samples. Thus, in ZIG the normalized count data is first performed a logarithmic transform to control the variability of taxonomic feature measurements across samples.
Let nA and nB denote the microbiome count data for samples A and B from two populations, respectively, each with m features (OTUs); and let cij denote the raw count for sample j and feature i and k(j) = I{j ∈ groupA} be the class indicator function. Then, the continuity-corrected log2 of the raw count data yij = log2(cij + 1) is modeled by the zero-inflated model as a mixture of a point mass at zero I{0}(y) and a count distribution fcount(y; μ, σ2) ∼ N(μ, σ2). Given mixture parameters πj, the density of the zero-inflated Gaussian distribution for feature i in sample j with sj total counts is given as
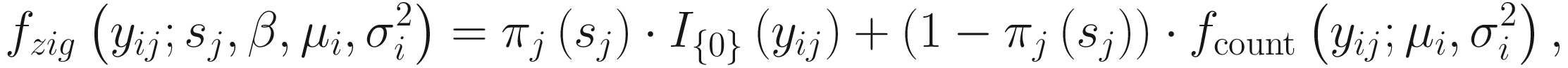
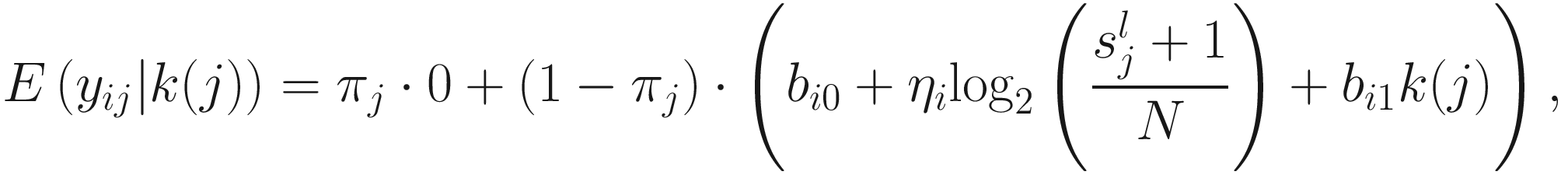
 term is used to capture OTU-specific normalization factors (e.g., feature-specific biases in PCR amplification) through parameter ηi. ZIG model can also be specified without OTU-specific normalization via including an offset term to serve as the normalization factor like in the linear model.
term is used to capture OTU-specific normalization factors (e.g., feature-specific biases in PCR amplification) through parameter ηi. ZIG model can also be specified without OTU-specific normalization via including an offset term to serve as the normalization factor like in the linear model.To model the dependency of the number of zero-valued features of a sample on its total number of counts, the mixture parameter πj(sj) is modeled as a binomial process:
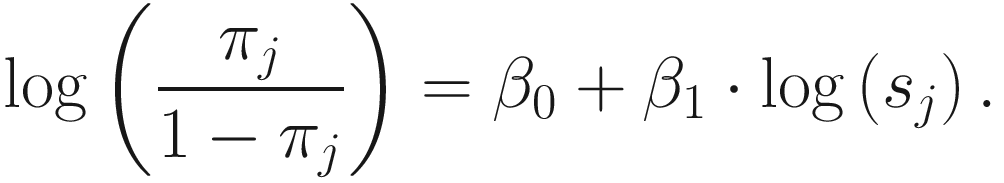
ZIG model was developed under the framework of linear modeling and standard conventions in DAA methods in gene expression; thus it has the advantage of controlling for confounding factors. Except the group membership variable, other clinical covariates can also be incorporated into the ZIG model to detect the confounding effect. Appropriate covariates can also be included to capture variability in the sampling process. The full set of estimates are denoted as θij = {β0, β1, bi0, ηi, bi1}. The mixture membership is treated as Δij = 1 if yij is generated from the zero point mass as latent indicator variables. Then the log likelihood in this extended model is given as
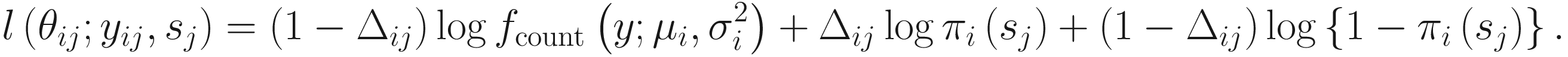
By this formation, this extended model is modeled as a mixture of a point mass at zero and a normal distribution, in which the part of the point mass at zero is used to model features (OTUs/taxa) that are usually sparse and have many zero counts and the normal distribution part is used to model the log transformed counts of the mean group abundance (the nonzero observed counts).The log maximum likelihood estimates are approximated by using the expectation-maximization algorithm. The function fitZig() estimates the probability whether a zero for a particular feature in a sample is a technical zero or not.
A moderated t-statistic fitFeatureModel is constructed to estimate fold change (b1i) (only for the count component of the ZIG mixture model) and its standard error by empirical Bayes shrinkage of parameter estimates (Smyth 2005). The P-values are obtained by a hypothesis testing the null of b1i = 0 using a parametric t-distribution. The zero-inflated log-normal model has been wrapped into the fitFeatureModel() to fit a zero-inflated model for each specific feature (OTU/ taxon) separately. Currently, fitFeatureModel() is only implementable to binary covariate case. The moderated t-statistic is defined as below:
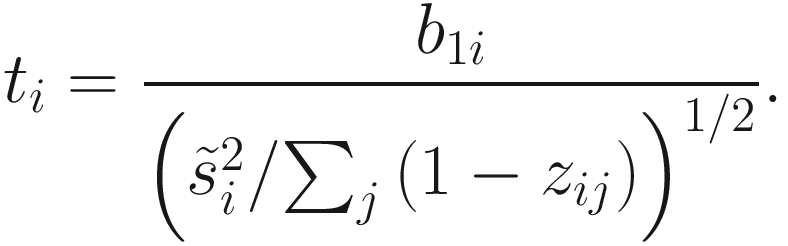
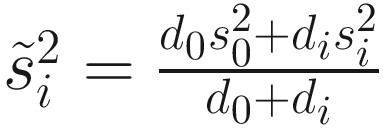 is obtained by pooling all features’ variances as described in Smyth (2005);
is obtained by pooling all features’ variances as described in Smyth (2005); 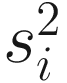 and di are the observed feature variance and degrees of freedom, respectively; and d0 and
and di are the observed feature variance and degrees of freedom, respectively; and d0 and  are estimated using the method of moments incorporating all feature variances and degrees of freedom, respectively. The multiple testing of features is corrected using the Q-value method (Storey and Tibshirani 2003). The choice of using a log-normal distribution in the count component of the mixture rather than a generalized linear model (e.g., negative binomial) in forming the fitFeatureModel() function is for computational efficiency and numerical stability as well as appropriateness of the log-normal distribution for the marker-gene survey study with moderate to large sample sizes (Soneson and Delorenzi 2013; Paulson et al. 2013).
are estimated using the method of moments incorporating all feature variances and degrees of freedom, respectively. The multiple testing of features is corrected using the Q-value method (Storey and Tibshirani 2003). The choice of using a log-normal distribution in the count component of the mixture rather than a generalized linear model (e.g., negative binomial) in forming the fitFeatureModel() function is for computational efficiency and numerical stability as well as appropriateness of the log-normal distribution for the marker-gene survey study with moderate to large sample sizes (Soneson and Delorenzi 2013; Paulson et al. 2013).12.2 Implement ZILN via metagenomeSeq
The metagenomeSeq package was designed to detect features (i.e., OTU, genus, species, etc.) that are differentially abundant between two or more groups of multiple samples. The software was also designed to implement the proposed CSS normalization technique and ZIG mixture model to account for sparsity due to under-sampling of microbial communities on disease association detection and testing of feature correlations (Paulson et al. 2013). The metagenomeSeq package implements two functions to (1) control for biases in measurements across taxonomic features via CSS and (2) account for varying depths of coverage via ZIG.
To facilitate modeling covariate effects or confounding sources of variability and interpreting results, the metagenomeSeq package uses linear model framework and provides a few visualization functions to examine discoveries. Generally, to implement metagenomeSeq, we need to take six steps: (1) load OTU, taxonomy data, and metadata; (2) create MRexperiment object; (3) normalize data via MRexperiment objects; (4) perform statistical testing of abundance or presence-absence; (5) visualize and save analysis results; and (6) visualize features. We illustrate how to implement ZIG using metagenomeSeq step by step as below.
We introduced this dataset in Example 9.1 (Zhang et al. 2020) and used it to illustrate calculations and statistical hypothesis testing of alpha and beta diversities in Chaps. 9, 10, and 11, respectively. Here we continue to use this dataset to illustrate the metagenomeSeq package.
Step 1: Load OTU table, annotated taxonomy data, and metadata.
sample1 | sample2 | … | samplen | |
|---|---|---|---|---|
feature1 | c11 | c12 | … | c1n |
feature2 | c21 | c22 | … | c2n |
. . . | ||||
featurem | cm1 | cm2 | … | cmn |
The above table presents m features in n samples, where the elements in a count matrix C (m, n), cij, are the number of reads annotated for a particular feature i (i.e., OTU, genus, species, etc.) in sample j.
To create a MRexperiment object, we need to load count data, taxonomy data, and metadata. First we set up working directory and install the metagenomeSeq package (version 1.36.0, April 10, 2022):
The metagenomeSeq package requires a feature table, which is a count matrix with features along rows and samples along the columns. We can use the loadMeta() function to load count data, which is tab-delimited OTU matrix. The loadMeta() function loads the taxa (OTUs) and counts into a list:
Now we load the tax table. It requires that the row order of OTUs in taxonomy table (matrix with tab-delimited format) must match the row order of OTUs in OTU table (matrix with tab-delimited format):
In above read.delim () function, specifying the argument “stringsAsFactors = FALSE” is important. By default, “stringsAsFactors” is set to TRUE in the read.delim() and other functions including read.table(), read.csv(), and read.csv2() when importing the columns containing character strings into R as factors. The reason for setting strings as factors is to tell R to treat categorical variables into individual dummy variables for modeling functions like lm() and glm(). However, in microbiome or genomics study, it doesn’t make sense to encode the names of the taxa or genes in one column of data as factors because they are essentially just labels and not to be used in any modeling function. So, we need to specify the “stringsAsFactors” argument into FALSE to change the default setting.
Phenotype data can be optionally loaded into R with loadPhenoData(). This function loads the data as a list. Now we use loadPhenoData () function to load the metadata into R:
Step 2: Create MRexperiment object.
assayData: contains matrices with equal dimensions and with column number equal to nrow(phenoData), which is an AssayData-class.
phenoData: contains experimenter-supplied variables describing sample (i.e., columns in assayData) phenotypes, which is an AnnotatedDataFrame-class.
featureData: contains variables describing features (i.e., rows in assayData) unique to this experiment, which is an AnnotatedDataFrame-class.
experimentData: contains details of experimental methods, which is a MIAME-class.
annotation: label associated with the annotation package used in the experiment, which is character.
protocolData: contains microarray equipment-generated variables describing sample (i.e., columns in assayData) phenotypes, which is an AnnotatedDataFrame-class.
The MRexperiment object uses a simple extension of eSet called expSummary (the S4 class with adding a single experiment summary slot, a data frame) to include the depth of coverage and the normalization factors for each sample. In MRexperiment object, the three main slots of assayData, phenoData, and featureData are most useful. All matrices are organized in the assayData slot, all phenotype data is stored in phenoData, and feature data (OTUs, taxonomic assignment to varying levels, etc.) is stored in featureData. Additional slots are available for reproducibility and annotation.
A MRexperiment object will be created by the function newMRexperiment(). This function takes a count matrix, phenoData (annotated data frame), and featureData (annotated data frame) as input. To create a MRexperiment object, call the newMRexperiment() and pass the counts, phenotype, and feature data as parameters. After the datasets are formatted as MRexperiment objects, the analysis is relatively easy using the metagenomeSeq package.
Below we create a MRexperiment object named “MRobj”. First, we convert both phenoData and featureData into data frames using the AnnotatedDataFrame() function:
Step 3: Normalize data via MRexperiment objects.
After the MRexperiment object was created, we can use the MRexperiment object to normalize the data, perform statistical tests (abundance or presence-absence), and visualize or save the analysis results.
- (i)
Calculate normalization factors using the function cumNorm().
First, check if the samples were normalized.
We can use the normFactors () function to access the normalization factors (aka the scaling factors) of samples in a MRexperiment object:
Second, calculate the proper percentile using the cumNormStat()and cumNormStatFast().
To calculate the proper percentile for which to sum counts up to and scale by, we can use either cumNormStat () or cumNormStatFast().
The cumNormStatFast() function is faster than the cumNormStat() function.
Third, calculate the scaling factors using the cumNorm ().
- (ii)
Calculate normalization factors using the function wrenchNorm ().
An alternative to normalizing counts (calculating normalization factors) using cumNorm is to use the wrenchNorm method. These two functions behave similarly; however, the difference is that the cumNorm method uses the percentile, while the wrenchNorm method takes the condition as argument. The condition is a factor with values that separate samples into phenotypic groups of interest (in this case, Group/Genotype). The authors of this package stated that when it is used appropriately, wrench normalization is preferable over cumulative normalization:
Step 4: Perform statistical testing of abundance.
The differential abundance analysis of features (e.g., OTUs) can be fitted using the functions fitFeatureModel() and fitZig(). The fitFeatureModel() was a latest development by reparametrizing the authors’ original zero-inflation model to fit zero-inflated log-normal mixture model for each feature (OTU) separately. The fitFeatureModel() was recommended over fitZig() in the metagenomeSeq package.
obj is a MRexperiment object with count data.
mod is used to specify the model for the count distribution.
coef is the coefficient of interest to grab log fold changes.
B is used to specify the number of bootstraps to perform. If B is specified greater than 1, then it performs permutation test.
szero (TRUE/FALSE) is used to shrink zero component parameters.
spos (TRUE/FALSE) is used to shrink positive component parameters.
After implementing the fitFeatureModel(), it returns a list of objects including call (the call made to fitFeatureModel), fitZeroLogNormal (a list of parameter estimates for the zero-inflated log-normal model), design (model matrix), taxa (taxa names), counts (count matrix), pvalues (calculated P-values), and permuttedfits (permutted z-score estimates under the null). The model outputs provide the useful summary tables: MRcoefs, MRtable, and MRfulltable.
Here, we use fitFeatureModel() to conduct hypothesis testing of mice microbiome differential abundance to compare the differences between genotype/group factors. This study was a longitudinal design with two measurements at before and post treatment. To illustrate this model, here we use the data at post treatment.
Step 5: Save and explore analysis results.
Modeling results using fitFeatureModel based on post-QtRNA mouse microbiome data
+Samples in group 0 | +samples in group 1 | Counts in group 0 | counts in group 1 | oddsRatio | Lower | Upper | FisherP | fisherAdjP | logFC | se | p-values | adjPvalues | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
OTU_126 | 2 | 10 | 3 | 10052 | 0 | 0 | 0.261985148691248 | 0.000714455822814956 | 0.0147177899499881 | 7.7572762392443 | 0.782297610849027 | 0 | 0 |
OTU_116 | 3 | 10 | 10 | 8130 | 0 | 0 | 0.388279386040879 | 0.00.309597523219815 | 0.0631475748194016 | 6.63063439517916 | 0.735958182613116 | 0 | 0 |
OTU_101 | 3 | 6 | 3 | 3058 | 0.305415044366772 | 0.030053635388153 | 2.46429182813556 | 0.369849964277209 | 1 | 5.390903521682831 | 1.24753104634402 | 2.17350999687227o-06 | 2.79839412097305o-05 |
OTU_125 | 1 | 10 | 2 | 3241 | 0 | 0 | 0.166690753277639 | 0.000119075970469159 | 0.00306620623958085 | 5.39137800592425 | 0.188856285124351 | 0 | 0 |
OTU_558 | 2 | 6 | 4 | 1863 | 0.184118110070328 | 0.0125264745480946 | 1.65925396045797 | 0.169802333889021 | 1 | 4.66860566955941 | 1.71741594144821 | 0.00656005395386594 | 0.0337842778624096 |
OTU_108 | 1 | 6 | 2 | 27889 | 0.0859350429538673 | 0.00146108353677648 | 1.05397598911988 | 0.0572755417956657 | 0.453798523457967 | 4.61985047754296 | 1.35624280574321 | 0.000658354420500995 | 0.00565087544263354 |
OTU_408 | 10 | 1 | 1044 | 1 | Inf | 5.9991330073025 | Inf | 0.000119075970469159 | 0.00306620623958085 | -4.32710318121278 | 0.33177493173258 | 0 | 0 |
OTU_323 | 0 | 10 | 0 | 527 | 0 | 0 | 0.0897995510045625 | 1.0825088224469o-05 | 0.00111498408712031 | 3.39310932393747 | 0.388662351098798 | 0 | 0 |
OTU_97 | 1 | 6 | 3 | 4689 | 0.0859350429538673 | 0.00146108353677648 | 1.05397598911988 | 0.0572755417956657 | 0.453798523457967 | 3.18079174547734 | 1.10745461114788 | 0.0040767078299202 | 0.02210000477095674 |
OTU_367 | 1 | 6 | 1 | 850 | 0.0859350429538673 | 0.00146108353677648 | 1.05397598911988 | 0.0572755417956657 | 0.453798523457967 | 2.67579145567032 | 0.78377736855131 | 0.000640239150733191 | 0.00565087544263354 |
Step 6: Visualize Features.
MetagenomeSeq has developed several plotting functions to help with visualization and analysis of datasets.
Step 6a: plotMRheatmap – heatmap of abundance estimates (Fig. 12.1).
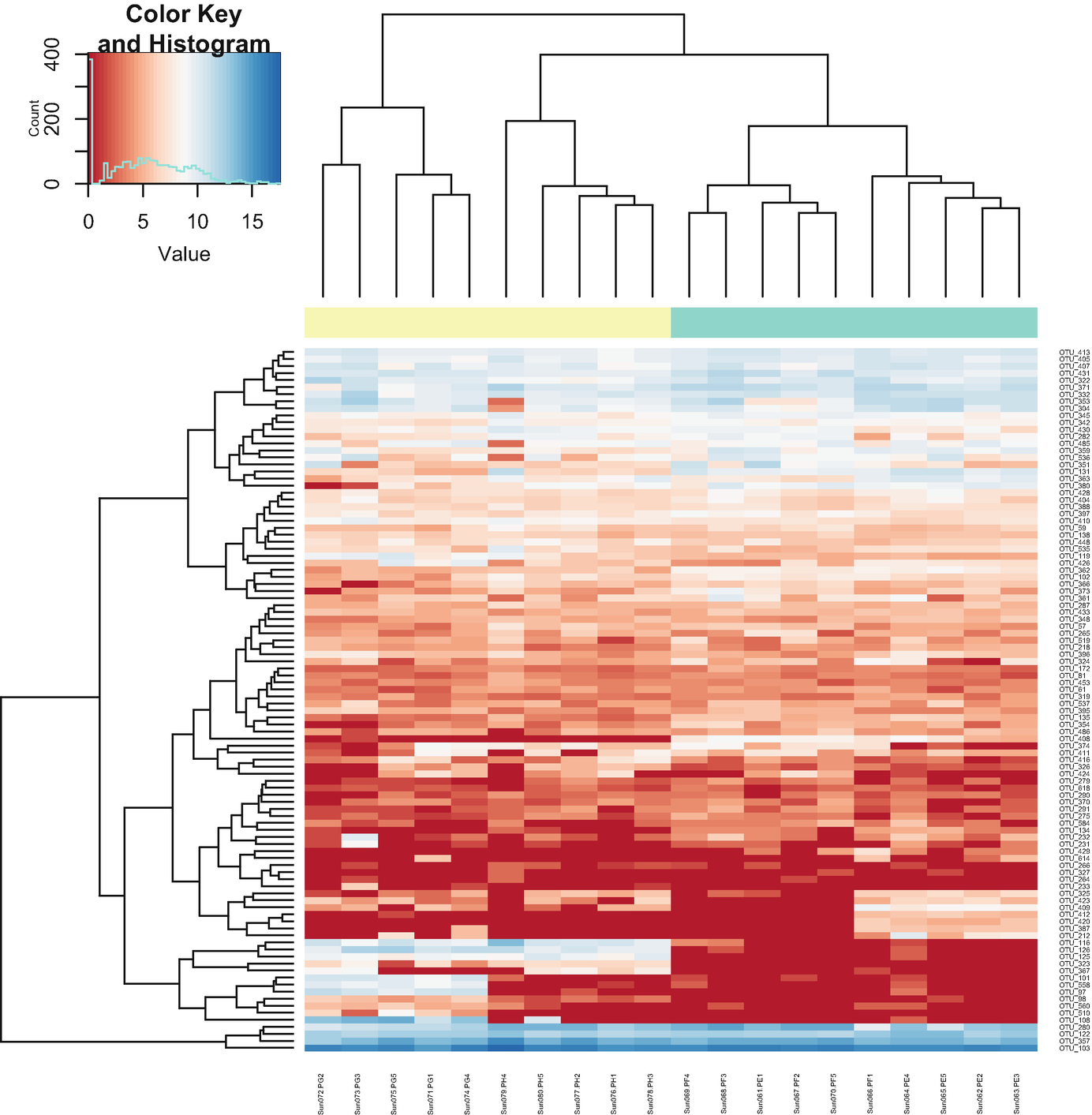
A heatmap and hierarchical cluster exhibit the abundance estimates. An inset graph of count versus value exposes the color key and histogram. The values are estimated between 0 and 15.
Heatmap of abundance estimates based on post-QtRNA mouse microbiome data
The above commands create a heatmap and hierarchical clustering of log2 transformed counts for the 100 OTUs with the largest overall variance. Red values indicate counts close to zero. Row color labels indicate OTU taxonomic class; column color labels indicate genotype (yellow = KO, green = WT). Notice that the samples are obviously clustered by genotypes.
Step 6b: plotCorr – heatmap of pairwise correlations (Fig. 12.2).
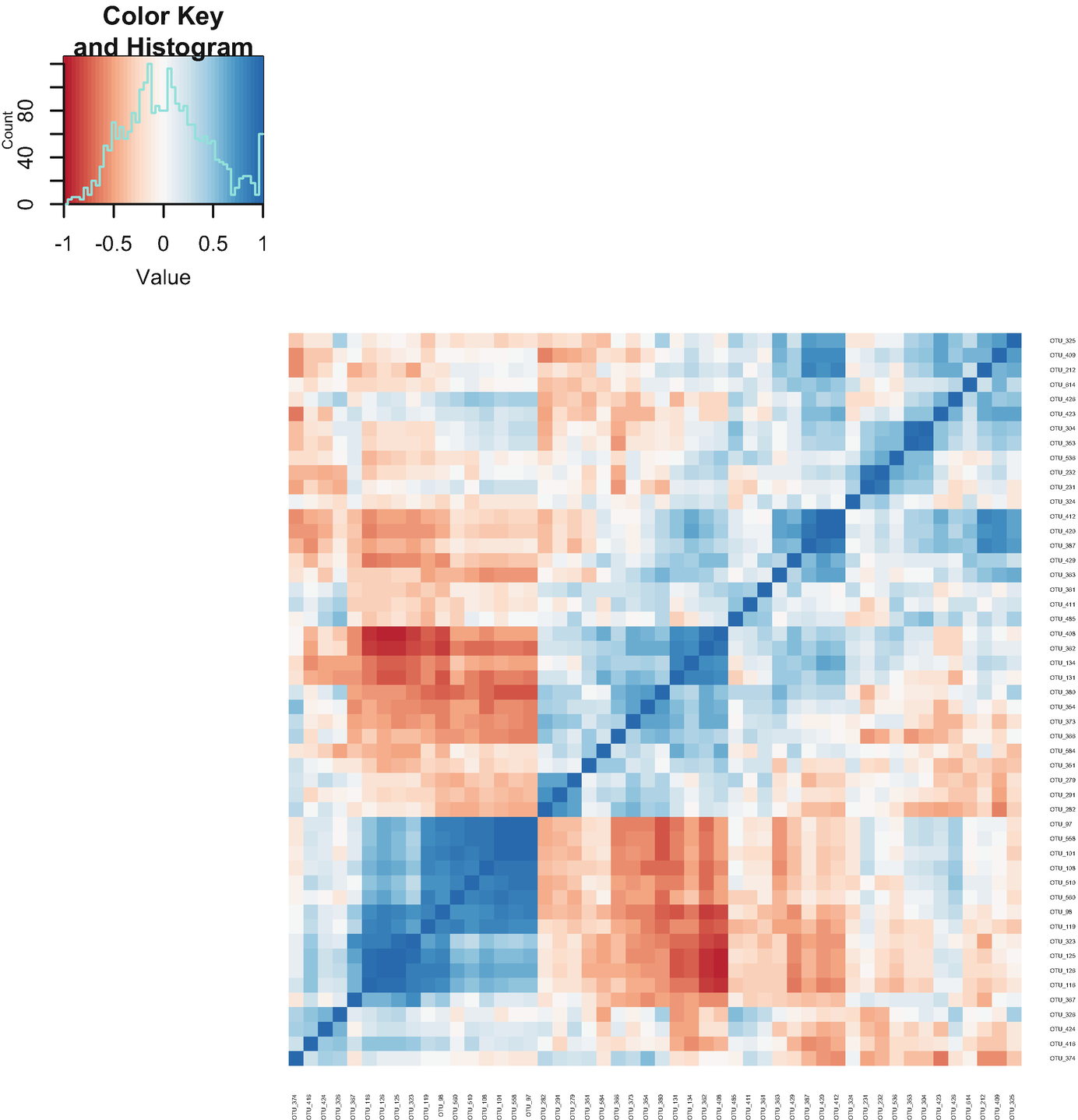
A heatmap exhibits the pairwise correlations. An inset graph of count versus value exposes the color key and histogram. The counts are estimated between 0 and 80.
Heatmap of pairwise correlations based on post-QtRNA mouse microbiome data
Step 6c: plotOrd – PCA/MDS components (Fig. 12.3).
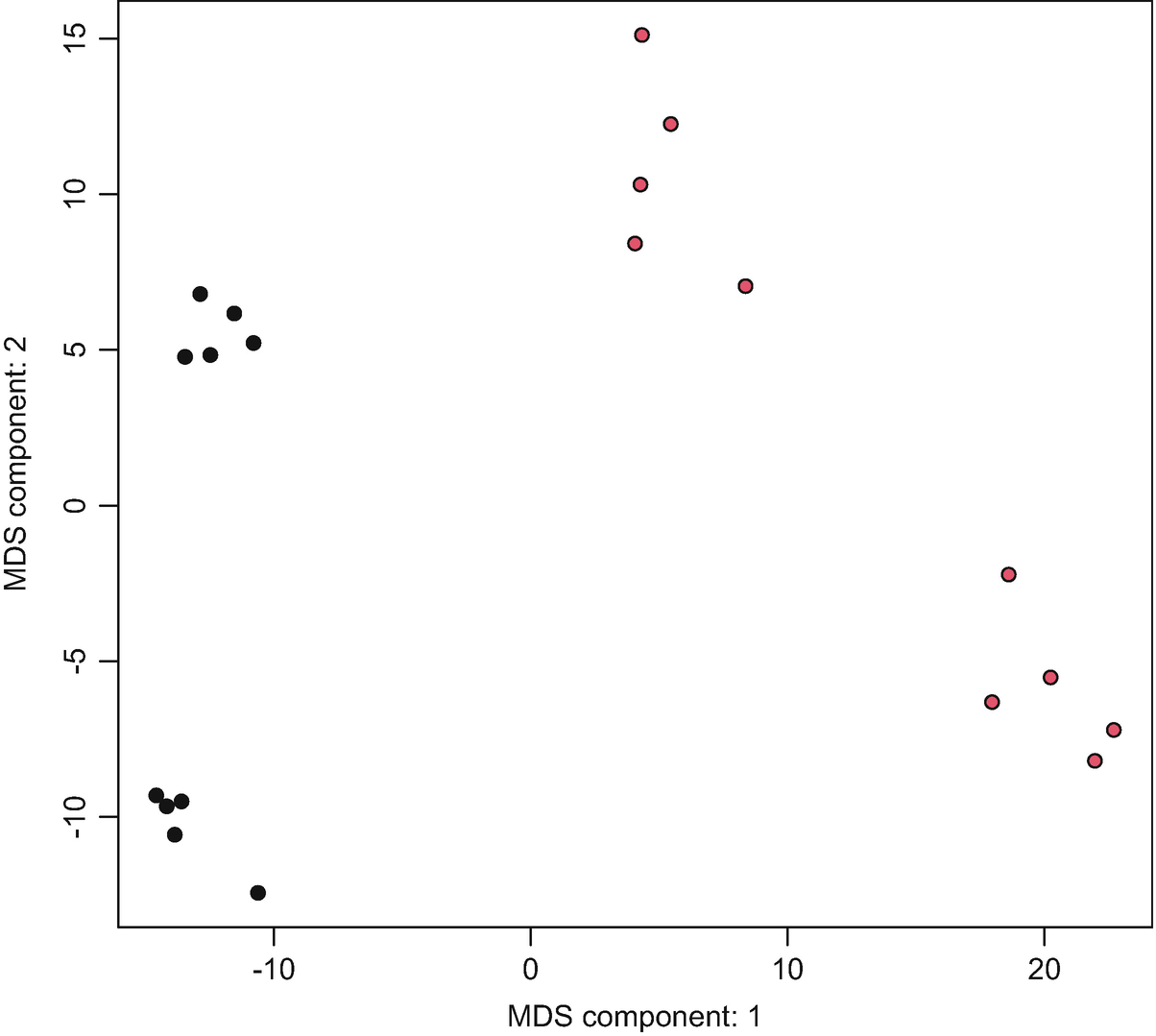
A graph of M D S component: 2 versus M D S component: 1 exhibits the C M D S plots. The plots were approximated between negative 10 to 20 along the x-axis and negative 10 to 15 along the y-axis.
Ordination plot with MDS components based on post-QtRNA mouse microbiome data
We can also load the vegan package and set distfun = vegdist and use dist.method = ‘bray’ to generate the PCA using the Bray-Curtis dissimilarity method.
12.3 Some Additional Statistical Tests in metagenomeSeq
Below we will illustrate some useful tests in the metagenomeSeq package.
12.3.1 Log-Normal Permutation Test of Abundance
We can fit the same model as above using a standard log-normal linear model to provide a permutation-based P-values. This method was originally used by metastats (White et al. 2009; Paulson et al. 2011) for non-sparse large samples. The fitLogNormal() function is a wrapper to perform the permutation test on the t-statistic. There is an option to choose the CSS normalization and use log2 transformation to transform the data. Here, we use 1000 permutations to provide P-value resolution to the thousandth. We specify the coefficient parameter equal to 2 to test the coefficient of interest (here, Group). A list of significant features is generated to hold the significant features:
12.3.2 Presence-Absence Testing of the Proportion/Odds
The presence-absence testing is implemented to test the hypothesis that the proportion/odds of a given feature presented is higher/lower among one group of individuals compared to another. The test uses the fitPA() to perform Fisher’s exact test to create a 2 × 2 contingency table and calculate P-values, odd’s ratios, and confidence intervals. The function accepts either a MRexperiment object or matrix as input data:
12.3.3 Discovery Odds Ratio Testing of the Proportion of Observed Counts
The discovery test is implemented to test the hypothesis that the proportion of observed counts for a feature of all counts are comparable between groups. The test uses the fitDO() to perform Fisher’s exact test to create a 2 × 2 contingency table and calculate P-values, odd’s ratios, and confidence intervals. The function accepts either a MRexperiment object or matrix as input data:
12.3.4 Perform Feature Correlations
We can implement correlationTest () and correctIndices() to conduct a pairwise test of the correlations of abundance features or samples for each row of a matrix or MRexperiment object. The function correlationTest () returns the basic Pearson, Spearman, Kendall correlation statistics for the rows of the input and the associated P-values. For a vector of length ncol(obj), this function also calculates the correlation of each row with the associated vector. However, we should be cautious when we infer correlation networks from genomic survey data (Friedman and Alm 2012):
12.4 Illustrate Some Useful Functions in metagenomeSeq
To facilitate analysis using the metagenomeSeq package, we illustrate some useful functions.
12.4.1 Access the MRexperiment Object
Three pairs of functions are used to access the raw or normalized count matrix, feature, and phenotype information, respectively. The MRcounts () function is used for accessing the raw or normalized count matrix, the featureData() and fData() functions are used for accessing feature information, and the phenoData() and pData() functions are used for accessing phenotype information.
We use the MRcounts() function to access the raw count matrix:
The feature information can be accessed with the featureData() and fData() functions. The differences are that the method of featureData() provides the S4 class information, while the method of fData() provides the information on data frame of taxonomy table:
The phenotype information can be accessed with the phenoData () and pData () functions. The differences are that the method of phenoData () provides the S4 class information, while the method of pData () provides the information on data frame of metadata table:
12.4.2 Subset the MRexperiment Object
We can subset the MRexperiment-class object. The following commands subset the object “MRobj” with row sum greater than 100 features for before-treatment samples:
Above outputs show that the sub-object has 20 samples in before-treatment.
12.4.3 Filter the MRexperiment Object or Count Matrix
We can use the filterData () function to filter the data to maintain a threshold of minimum depth or OTU presence. The following commands filter the data based on presenting 1 number of features after filtering samples by at least depth of coverage 100. This function can be conducted on a MRexperiment object or count matrix:
12.4.4 Merge the MRexperiment Object
12.4.5 Call the Normalized Counts Using the cumNormMat() and MRcounts()
Below we use the function cumNormMat() to return the normalized matrix using the percentile generated by the cumNormStatFast () function and scale by 1000:
Below we use the function MRcounts () to access the counts slot of a MRexperiment object. The counts slot holds the raw count data representing (along the rows) the number of reads annotated for a particular feature and (along the columns) the sample.
12.4.6 Calculate the Normalization Factors Using the calcNormFactors()
12.4.7 Access the Library Sizes Using the libSize()
12.4.8 Save the Normalized Counts Using the exportMat()
The exportMat() function exports the normalized MRexperiment dataset as a matrix.
12.4.9 Save the Sample Statistics Using the exportStats()
The exportStats () function exports a matrix of values for each sample including various sample statistics: sample ids, the sample scaling factor, quantile value, the number identified features, and library size (depth of coverage):
12.4.10 Find Unique OTUs or Features
We can use the function uniqueFeatures () to find features absent from any number of classes. The returned table lists the feature ids, the number of positive features, and reads for each group. Thresholding for the number of positive samples or reads required are options:
12.4.11 Aggregate Taxa
Normalization is recommended at the OTU level. However, the count matrix (either normalized or not) can be aggregated based on a particular user-defined level of taxonomy. Currently, there are two functions called aggregateByTaxonomy() and aggTax() in the metagenomicsSeq package for using the feature-data information in the MRexperiment object to aggregate taxa. The aggregateByTaxonomy() and aggTax() are used to aggregate a MRexperiment object or count matrix to a particular level. We first call the aggregateByTaxonomy() function on the MRexperiment object obj_Post to aggregate the “Genus” level (a featureData column) counts using the default colSums () function:
We then call the aggTax () function on the MRexperiment object obj_Post to aggregate the “Phylum” level (a featureData column) counts using the default colSums () function:
12.4.12 Aggregate Samples
Samples can also be aggregated using the phenoData information in the MRexperiment object. Currently, there are two functions called aggregateBySample() and aggSamp() in the metagenomicsSeq package for using the phenoData information in the MRexperimen to aggregate a MRexperiment object or count matrix to by a factor.
In the following commands, we first call the aggregateBySample() function on the MRexperiment object obj_Post to use the Group (a phenoData column name) to aggregate counts with the default rowMeans () aggregating function:
In microbiome data analysis, the data is often required to be aggregated. The functions aggregateByTaxonomy(), aggregateBySample(), aggTax(), and aggSamp() are very flexible. They can facilitate data in either a matrix with a vector of labels or a MRexperiment object with a vector of labels or featureData column name. All these functions can output either a matrix or MRexperiment object.
12.5 Remarks on CSS Normalization, ZIG, and ZILN
CSS method divides raw counts into the cumulative sum of counts up to a percentile determined using a data-driven approach, which is an adaptive extension of the quantile normalization method (Bullard et al. 2010). CSS normalization may have the advantages, including the following: (1) CSS may have superior performance for weighted metrics, although it is arguable (Paulson et al. 2013, 2014; Costea et al. 2014; Weiss et al. 2017). (2) CSS is similar to log upper quartile (LUQ), but it is flexible than LUQ because it allows a dependent threshold to determine each sample’s quantile divisor (Weiss et al. 2017). (3) It was shown that CSS along with GMPR is overall more robust to sample-specific outlier OTUs than TSS and RNA-seq normalization methods (Chen et al. 2018). For CSS, it is crucial to ensure that chosen quantile is appropriate so that the normalization approach does not introduce normalization-related artifacts in the data, in which the normalization method assumes that all the count distributions of samples are roughly equivalent and independent of each other up to this quantile. However, the challenge is that the percentiles that CSS is based on could not be determined for microbiome datasets with high variable counts (Chen et al. 2018).
- 1.
It was shown that metagenomeSeq outperforms other widely used statistical methods in the field including Metastats (White et al. 2009), LEfSe’s Kruskal-Wallis test (Segata et al. 2011), and representative methods for RNA-seq analysis, edgeR (Robinson et al. 2010) and DESeq (Anders and Huber 2010) in terms of the area under the curve (AUC) scores (Paulson et al. 2013). Others also showed that metagenomeSeq has slightly higher powers than most of the other DA methods (Lin and Peddada 2020b). (2) It yields a more precise biological interpretation of microbiome data (Paulson et al. 2013). (3) ZIG performs well when there is an adequate number of biological replicates (McMurdie and Holmes 2014).
However, the disadvantages of ZIG include a higher false-positive rate (FDR) (McMurdie and Holmes 2014; Mandal et al. 2015; Weiss et al. 2017), and the problem of FDR inflation gets worse when sample size or the effect size (i.e., fold change of mean absolute abundances) increases (Weiss et al. 2017; Lin and Peddada 2020a). This disadvantage is mostly criticized in microbiome literature; currently it was shown that ZIG is subject to inflate FDR even with the normalized observed abundances by its built-in scaling method (CSS) (Lin and Peddada 2020b).
However, we should point out that some evaluated disadvantages of ZIG and ZILN were based on compositional approach. In microbiome literature, the compositional approach is also arguable. Additionally, ZIG was shown increasing FDR that was assessed, using rarefied data (McMurdie and Holmes 2014; Weiss et al. 2017). This also highlights the difference between count-based (e.g., ZIG) and compositional approach. ZIG was developed for 16S count data, and thus it is reasonable that it is not suitable for compositional or proportion data. ZIG and its CSS require original library size to capture the zero proportions. Rarefying biological count data omits available valid data, and hence it is statistically inadmissible (McMurdie and Holmes 2014). Therefore, criticizing ZIG based on rarefying is not a strong argument because the use of rarefication itself is also arguable.
- 2.
ZIG was developed with the log transformation on the read counts using an empirical Bayes procedure to estimate the moderated variances. This was reviewed it is not clear how to extend the empirical Bayes method in longitudinal setting and is not trivial to simply include certain random effects by extending these methods (Chen and Li 2016).
- 3.
MetagenomeSeq is specifically developed for handling the high number of zero observations encountered in metagenomic data. However, inference is done after transformation using a log transformation (log2(yij + 1)) followed by correction for zero inflation based on a Gaussian mixture model (Paulson et al. 2013). Thus, actually metagenomeSeq moderates the gene-specific variance estimates (Smyth 2004) by some kind of removing zeros.
So far, most performances of metagenomeSeq have been evaluated based on ZIG; recently, one study demonstrated that ZILN mixture model successfully controls the FDR under 5% in all simulations, but suffers a severe loss of power (Lin and Peddada 2020a). Additional evaluations based on the ZILN are needed for providing further information on the metagenomeSeq methods.
12.6 Summary
In this chapter, we focused on introducing the metagenomeSeq methods including ZIG and ZILN mixture models as well as additional statistical tests and useful functions in metagenomeSeq. We first introduced TSS and CSS normalization methods. CSS is one critical component of the metagenomeSeq methods. We then described the ZIG and ZILN models. Next, we illustrated how to implement ZILN via the metagenomeSeq package. Currently ZILN or fitFeatureModel() function is recommended for use over ZIG functions or fitZig() function in the metagenomeSeq manual. Followed that, we illustrated some additional statistical tests that are available in metagenomeSeq: log-normal permutation test of abundance, presence-absence testing of the proportion/odds, discovery odds ratio testing of the proportion of observed counts, as well as performing feature correlations. To facilitate analysis of microbiome using the metagenomeSeq methods, we also illustrated some useful functions in metagenomeSeq to access the MRexperiment object, subset the MRexperiment object, filter the MRexperiment object or count matrix, merge the MRexperiment object, call the normalized counts using the cumNormMat() and MRcounts(), calculate the normalization factors using the calcNormFactors(), access the library sizes using the libSize(), save the normalized counts using the exportMat(), save the sample statistics using the exportStats(), find unique OTUs or features, and aggregate taxa and samples. Finally, we provided some remarks on CSS, ZIG, and ZILN.
In Chap. 13, we will introduce zero-inflated beta models for microbiome data.